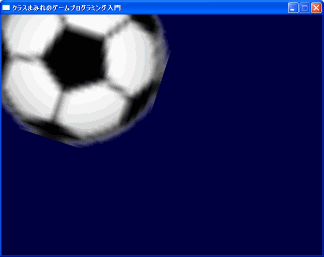
23:スプライトの回転処理

　スプライトの回転処理も幾何変換で行うことができます。拡大縮小処理と同じく、座標軸の原点を中心に回転が行われますので、行列の掛け合わせの順番は間違えの無いようにしなくてはいけません。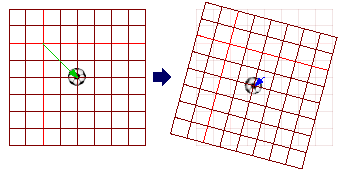


[先に移動を行うと、回転時に想定している場所からずれてしまう]
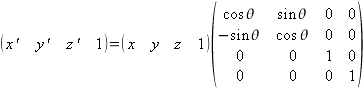
　回転を行う行列はこのようになります。値の代入はD3DXMatrixRotationZを使います。


[θはz軸周りの回転角度]

　数学になれていない人は、角度の指定は弧度法（360° = 2πで計算する方法）で行われることに注意してください。例えば45°の時計回りの回転を行う場合はθに(π / 2)を代入します。度数法から弧度法に変換する関数を「GameObject.h」に用意しておいてもよいでしょう。C++はマクロの発展であるインライン関数という機能が用意されています。指定した文字列に強引に置き換えるマクロと違い、引数や戻り値の型を明確にできるので、数行程度の数値計算などに用いると大変便利です。ちなみに円周率πはDirectXでD3DX_PIマクロとして定義されています。
inline.h
// dは度数法による角度（°）、戻り値は弧度法による角度（rad）
inline float d2r(float d)
{
    return (d / 180.0f * D3DX_PI);
}
　では、Draw()に回転の要素も加えた関数を追加することにしましょう。最小の引数指定で済むように、拡大移動のみの描画、回転移動のみの描画などを用意し、最終的にはすべてのパラメータを指定する関数へ渡すようにしています。
sprite.h
CSprite : public CGameObject
{
private:
    /* 省略 */
    
public:
    /* 省略 */

    void Draw(float x, float y, int alpha = 255);
    void Draw(float x, float y, float r, int alpha = 255);
    void Draw(float x, float y, float ex, float ey, int alpha = 255);
    void Draw(float x, float y, float ex, float ey, float r, int alpha = 255);
};
sprite.cpp
void CSprite::Draw(float x, float y, int alpha)
{
    Draw(x, y, 1.0f, 1.0f, 0.0f, alpha);
}

void CSprite::Draw(float x, float y, float ex, float ey, int alpha)
{
    Draw(x, y, ex, ey, 0.0f, alpha);
}

void CSprite::Draw(float x, float y, float r, int alpha)
{
    Draw(x, y, 1.0f, 1.0f, r, alpha);
}

void CSprite::Draw(float x, float y, float ex, float ey, float r, int alpha)
{
    if(texture == NULL){
        DXTRACE_MSG(_T("テクスチャが読み込まれていません"));
        return;
    }

    D3DXMATRIX mtrx1, mtrx2;

    // 原点を重ね合わせる平行移動
    D3DXMatrixTranslation(&mtrx1, -orig_x, -orig_y, 0.0f);

    // 拡大行列と合成
    if(ex != 1.0f || ey != 1.0f){
        D3DXMatrixScaling(&mtrx2, ex, ey, 1.0f);
        D3DXMatrixMultiply(&mtrx1, &mtrx1, &mtrx2);
    }

    // 回転行列との合成
    if(r != 0.0f){
        D3DXMatrixRotationZ(&mtrx2, r);
        D3DXMatrixMultiply(&mtrx1, &mtrx1, &mtrx2);
    }

    // 指定の場所へ移動する行列との合成
    D3DXMatrixTranslation(&mtrx2, x, y, 0.0f);
    D3DXMatrixMultiply(&mtrx1, &mtrx1, &mtrx2);


    pSprite->Begin(NULL);

    pSprite->SetTransform(&mtrx1);
    pSprite->Draw(texture->GetTexture(), &drawrect, NULL, NULL, 0x00FFFFFF | ((BYTE)alpha << 24));

    pSprite->End();
}
　回転は指定した原点を軸に行われます。ヘリコプターのプロペラは中心を原点に、サーチライトは隅を原点になど、臨機応変に使い分けてみましょう。

←前の項目 次の項目→